free men
فريق العمـــــل *****

التوقيع : 
عدد الرسائل : 1500
الموقع : center d enfer
تاريخ التسجيل : 26/10/2009
وســــــــــام النشــــــــــــــاط : 6
 | |  Philosophical questions for IP Philosophical questions for IP | |
This section collects some problems for IP noted in the literature. 3.1 DilationConsider two logically unrelated propositions [ltr]H[/ltr] and [ltr]X[/ltr]. Now consider the four “state descriptions” of this simple model as set out in Figure 1. So [ltr]a=H∩X[/ltr] and so on. Now define [ltr]Y=a∪d[/ltr]. Alternatively, consider three propositions related in the following way: [ltr]Y[/ltr] is defined as “[ltr]H[/ltr] if and only if [ltr]X[/ltr]”.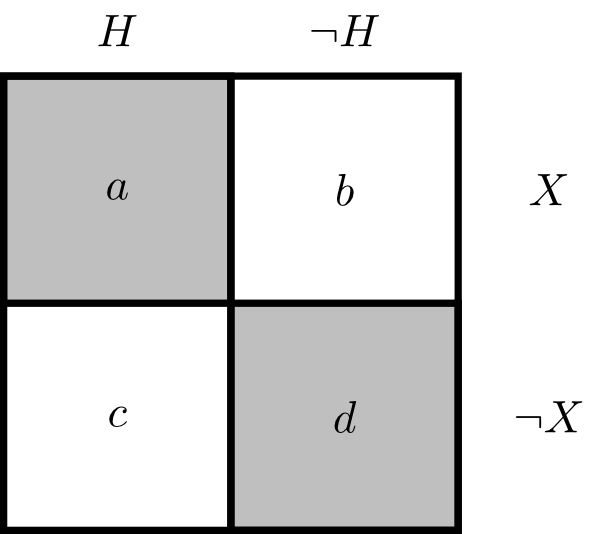
Figure 1: A diagram of the relationships after Seidenfeld (1994); [size=14][ltr][size=16]Y[/ltr] is the shaded area[/size][/size] Further imagine that [ltr]p(H∣X)=p(H)=1/2[/ltr]. No other relationships between the propositions hold except those required by logic and probability theory. It is straightforward to verify that the above constraints require that [ltr]p(Y)=1/2[/ltr]. The probability for [ltr]X[/ltr], however, is unconstrained.Let’s imagine you were given the above information, and took your representor to be the full set of probability functions that satisfied these constraints. Roger White suggested an intuitive gloss on how you might receive information about propositions so related and so constrained (White 2010). White’s puzzle goes like this. I have a proposition [ltr]X[/ltr], about which you know nothing at all. I have written whichever is true out of [ltr]X[/ltr] and [ltr]¬X[/ltr] on the Heads side of a fair coin. I have painted over the coin so you can’t see which side is heads. I then flip the coin and it lands with the [ltr]X[/ltr]uppermost. [ltr]H[/ltr] is the proposition that the coin lands heads up. [ltr]Y[/ltr] is the proposition that the coin lands with the “[ltr]X[/ltr]” side up.Imagine if you had a precise prior that made you certain of [ltr]X[/ltr] (this is compatible with the above constraints since [ltr]X[/ltr] was unconstrained). Seeing [ltr]X[/ltr] land uppermost now should be evidence that the coin has landed heads. The game set-up makes it such that these apparently irrelevant instances of evidence can carry information. Likewise, being very confident of [ltr]X[/ltr] makes [ltr]Y[/ltr] very good evidence for [ltr]H[/ltr]. If instead you were sure [ltr]X[/ltr] was false, [ltr]Y[/ltr] would be solid gold evidence of [ltr]H[/ltr]’s falsity. So it seems that [ltr]p(H∣Y)[/ltr] is proportional to prior belief in [ltr]X[/ltr] (indeed, this can be proven rather easily). Given the way the events are related, observing whether [ltr]X[/ltr] or [ltr]¬X[/ltr] landed uppermost is a noisy channel to learn about whether or not [ltr]H[/ltr] landed uppermost.So let’s go back to the original imprecise case and consider what it means to have an imprecise belief in [ltr]X[/ltr]. Among other things, it means considering possible that [ltr]X[/ltr] could be very likely. It is consistent with your belief state that [ltr]X[/ltr] is such that if you knew what proposition [ltr]X[/ltr] was, you would consider it very likely. In this case, [ltr]Y[/ltr] would be good evidence for [ltr]H[/ltr]. Note that in this case learning that the coin landed [ltr]¬X[/ltr] uppermost—call this [ltr]Y[size=13]′[/ltr]—would be just as good evidence against [ltr] H[/ltr]. Likewise, [ltr] X[/ltr] might be a proposition that you would have very low credence in, and thus [ltr] Y[/ltr] would be evidence against [ltr] H[/ltr].[/size] Since you are in a state of ignorance with respect to [ltr]X[/ltr], your representor contains probabilities that take [ltr]Y[/ltr] to be good evidence that [ltr]H[/ltr] and probabilities that take [ltr]Y[/ltr] to be good evidence that [ltr]¬H[/ltr]. So, despite the fact that [ltr]P(H)={1/2}[/ltr] we have [ltr]P(H∣Y)=[0,1][/ltr]. This phenomenon—posteriors being wider than their priors—is known as dilation. The phenomenon has been thoroughly investigated in the mathematical literature (Walley 1991; Seidenfeld and Wasserman 1993; Herron, Seidenfeld, and Wasserman 1994; Pedersen and Wheeler 2014). Levi and Seidenfeld reported an example of dilation to Good following Good (1967). Good mentioned this correspondence in his follow up paper (Good 1974). Recent interest in dilation in the philosophical community has been generated by White’s paper (White 2010).White considers dilation to be a problem since learning [ltr]Y[/ltr] doesn’t seem to be relevant to [ltr]H[/ltr]. That is, since you are ignorant about [ltr]X[/ltr], learning whether or not the coin landed [ltr]X[/ltr] up doesn’t seem to tell you anything about whether the coin landed heads up. It seems strange to argue that your belief in [ltr]H[/ltr] should dilate from [ltr]1/2[/ltr] to [ltr][0,1][/ltr] upon learning [ltr]Y[/ltr]. It feels as if this should just be irrelevant to [ltr]H[/ltr]. However, [ltr]Y[/ltr] is only really irrelevant to [ltr]H[/ltr] when [ltr]p(X)=1/2[/ltr]. Any other precise belief you might have in [ltr]X[/ltr] is such that [ltr]Y[/ltr] now affects your posterior belief in [ltr]H[/ltr]. Figure 2 shows the situation for one particular belief about how likely [ltr]X[/ltr] is; for one particular [ltr]p∈P[/ltr]. The horizontal line can shift up or down, depending on what the committee member we focus on believes about [ltr]X[/ltr]. [ltr]p(H∣Y)[/ltr] is a half only if the prior in [ltr]X[/ltr] is also a half. However, the imprecise probabilist takes into account all the ways [ltr]Y[/ltr] might affect belief in [ltr]H[/ltr].
Figure 2: A member of the credal committee (after Joyce (2011)) | |
|


