free men
فريق العمـــــل *****

التوقيع : 
عدد الرسائل : 1500
الموقع : center d enfer
تاريخ التسجيل : 26/10/2009
وســــــــــام النشــــــــــــــاط : 6
 | |  Determinism and Chaos Determinism and Chaos | |
If the world were governed by strictly deterministic laws, might it still look as though indeterminism reigns? This is one of the difficult questions that chaos theory raises for the epistemology of determinism.A deterministic chaotic system has, roughly speaking, two salient features: (i) the evolution of the system over a long time period effectively mimics a random or stochastic process—it lacks predictability or computability in some appropriate sense; (ii) two systems with nearly identical initial states will have radically divergent future developments, within a finite (and typically, short) timespan. We will use “randomness” to denote the first feature, and “sensitive dependence on initial conditions” (SDIC) for the latter. Definitions of chaos may focus on either or both of these properties; Batterman (1993) argues that only (ii) provides an appropriate basis for defining chaotic systems.A simple and very important example of a chaotic system in both randomness and SDIC terms is the Newtonian dynamics of a pool table with a convex obstacle (or obstacles) (Sinai 1970 and others). See Figure 1.
Figure 1: Billiard table with convex obstacleThe usual idealizing assumptions are made: no friction, perfectly elastic collisions, no outside influences. The ball's trajectory is determined by its initial position and direction of motion. If we imagine a slightly different initial direction, the trajectory will at first be only slightly different. And collisions with the straight walls will not tend to increase very rapidly the difference between trajectories. But collisions with the convex object will have the effect of amplifying the differences. After several collisions with the convex body or bodies, trajectories that started out very close to one another will have become wildly different—SDIC.In the example of the billiard table, we know that we are starting out with a Newtonian deterministic system—that is how the idealized example is defined. But chaotic dynamical systems come in a great variety of types: discrete and continuous, 2-dimensional, 3-dimensional and higher, particle-based and fluid-flow-based, and so on. Mathematically, we may suppose all of these systems share SDIC. But generally they will also display properties such as unpredictability, non-computability, Kolmogorov-random behavior, and so on—at least when looked at in the right way, or at the right level of detail. This leads to the following epistemic difficulty: if, in nature, we find a type of system that displays some or all of these latter properties, how can we decide which of the following two hypotheses is true?[list="margin-top: 0.5em; color: rgb(26, 26, 26); font-family: serif; font-size: 16.5px; line-height: 21px; background-color: rgb(255, 255, 255);"] [*]The system is governed by genuinely stochastic, indeterministic laws (or by no laws at all), i.e., its apparent randomness is in fact real randomness. [*]The system is governed by underlying deterministic laws, but is chaotic. [/list] In other words, once one appreciates the varieties of chaotic dynamical systems that exist,mathematically speaking, it starts to look difficult—maybe impossible—for us to ever decide whether apparently random behavior in nature arises from genuine stochasticity, or rather from deterministic chaos. Patrick Suppes (1993, 1996) argues, on the basis of theorems proven by Ornstein (1974 and later) that “There are processes which can equally well be analyzed as deterministic systems of classical mechanics or as indeterministic semi-Markov processes, no matter how many observations are made.” And he concludes that “Deterministic metaphysicians can comfortably hold to their view knowing they cannot be empirically refuted, but so can indeterministic ones as well.” (Suppes 1993, p. 254) For more recent works exploring the extent to which deterministic and indeterministic model systems may be regarded as empirically indistinguishable, see Werndl (2016) and references therein.There is certainly an interesting problem area here for the epistemology of determinism, but it must be handled with care. It may well be true that there are some deterministic dynamical systems that, when viewed properly, display behavior indistinguishable from that of a genuinely stochastic process. For example, using the billiard table above, if one divides its surface into quadrants and looks at which quadrant the ball is in at 30-second intervals, the resulting sequence is no doubt highly random. But this does not mean that the same system, when viewed in adifferent way (perhaps at a higher degree of precision) does not cease to look random and instead betray its deterministic nature. If we partition our billiard table into squares 2 centimeters a side and look at which quadrant the ball is in at .1 second intervals, the resulting sequence will be far from random. And finally, of course, if we simply look at the billiard table with our eyes, and see it as a billiard table, there is no obvious way at all to maintain that it may be a truly random process rather than a deterministic dynamical system. (See Winnie (1996) for a nice technical and philosophical discussion of these issues. Winnie explicates Ornstein's and others' results in some detail, and disputes Suppes' philosophical conclusions.)The dynamical systems usually studied under the label of “chaos” are usually either purely abstract, mathematical systems, or classical Newtonian systems. It is natural to wonder whether chaotic behavior carries over into the realm of systems governed by quantum mechanics as well. Interestingly, it is much harder to find natural correlates of classical chaotic behavior in true quantum systems (see Gutzwiller 1990). Some, at least, of the interpretive difficulties of quantum mechanics would have to be resolved before a meaningful assessment of chaos in quantum mechanics could be achieved. For example, SDIC is hard to find in the Schrödinger evolution of a wavefunction for a system with finite degrees of freedom; but in Bohmian quantum mechanics it is handled quite easily on the basis of particle trajectories (see Dürr, Goldstein and Zhangì 1992).The popularization of chaos theory in the relatively recent past perhaps made it seem self-evident that nature is full of genuinely chaotic systems. In fact, it is far from self-evident that such systems exist, other than in an approximate sense. Nevertheless, the mathematical exploration of chaos in dynamical systems helps us to understand some of the pitfalls that may attend our efforts to know whether our world is genuinely deterministic or not. 3.4 Metaphysical argumentsLet us suppose that we shall never have the Final Theory of Everything before us—at least in our lifetime—and that we also remain unclear (on physical/experimental grounds) as to whether that Final Theory will be of a type that can or cannot be deterministic. Is there nothing left that could sway our belief toward or against determinism? There is, of course: metaphysical argument. Metaphysical arguments on this issue are not currently very popular. But philosophical fashions change at least twice a century, and grand systemic metaphysics of the Leibnizian sort might one day come back into favor. Conversely, the anti-systemic, anti-fundamentalist metaphysics propounded by Cartwright (1999) might also come to predominate. As likely as not, for the foreseeable future metaphysical argument may be just as good a basis on which to discuss determinism's prospects as any arguments from mathematics or physics.4. The Status of Determinism in Physical TheoriesJohn Earman's Primer on Determinism (1986) remains the richest storehouse of information on the truth or falsity of determinism in various physical theories, from classical mechanics to quantum mechanics and general relativity. (See also his recent update on the subject, “Aspects of Determinism in Modern Physics” (2007)). Here I will give only a brief discussion of some key issues, referring the reader to Earman (1986) and other resources for more detail. Figuring out whether well-established theories are deterministic or not (or to what extent, if they fall only a bit short) does not do much to help us know whether our world is really governed by deterministic laws; all our current best theories, including General Relativity and the Standard Model of particle physics, are too flawed and ill-understood to be mistaken for anything close to a Final Theory. Nevertheless, as Earman stressed, the exploration is very valuable because of the way it enriches our understanding of the richness and complexity of determinism. 4.1 Classical mechanicsDespite the common belief that classical mechanics (the theory that inspired Laplace in his articulation of determinism) is perfectly deterministic, in fact the theory is rife with possibilities for determinism to break down. One class of problems arises due to the absence of an upper bound on the velocities of moving objects. Below we see the trajectory of an object that is accelerated unboundedly, its velocity becoming in effect infinite in a finite time. See Figure 2:
Figure 2: An object accelerates so as to reach spatial infinity in a finite timeBy the time t = t*, the object has literally disappeared from the world—its world-line never reaches the t = t* surface. (Never mind how the object gets accelerated in this way; there are mechanisms that are perfectly consistent with classical mechanics that can do the job. In fact, Xia (1992) showed that such acceleration can be accomplished by gravitational forces from only 5 finite objects, without collisions. No mechanism is shown in these diagrams.) This “escape to infinity,” while disturbing, does not yet look like a violation of determinism. But now recall that classical mechanics is time-symmetric: any model has a time-inverse, which is also a consistent model of the theory. The time-inverse of our escaping body is playfully called a “space invader.”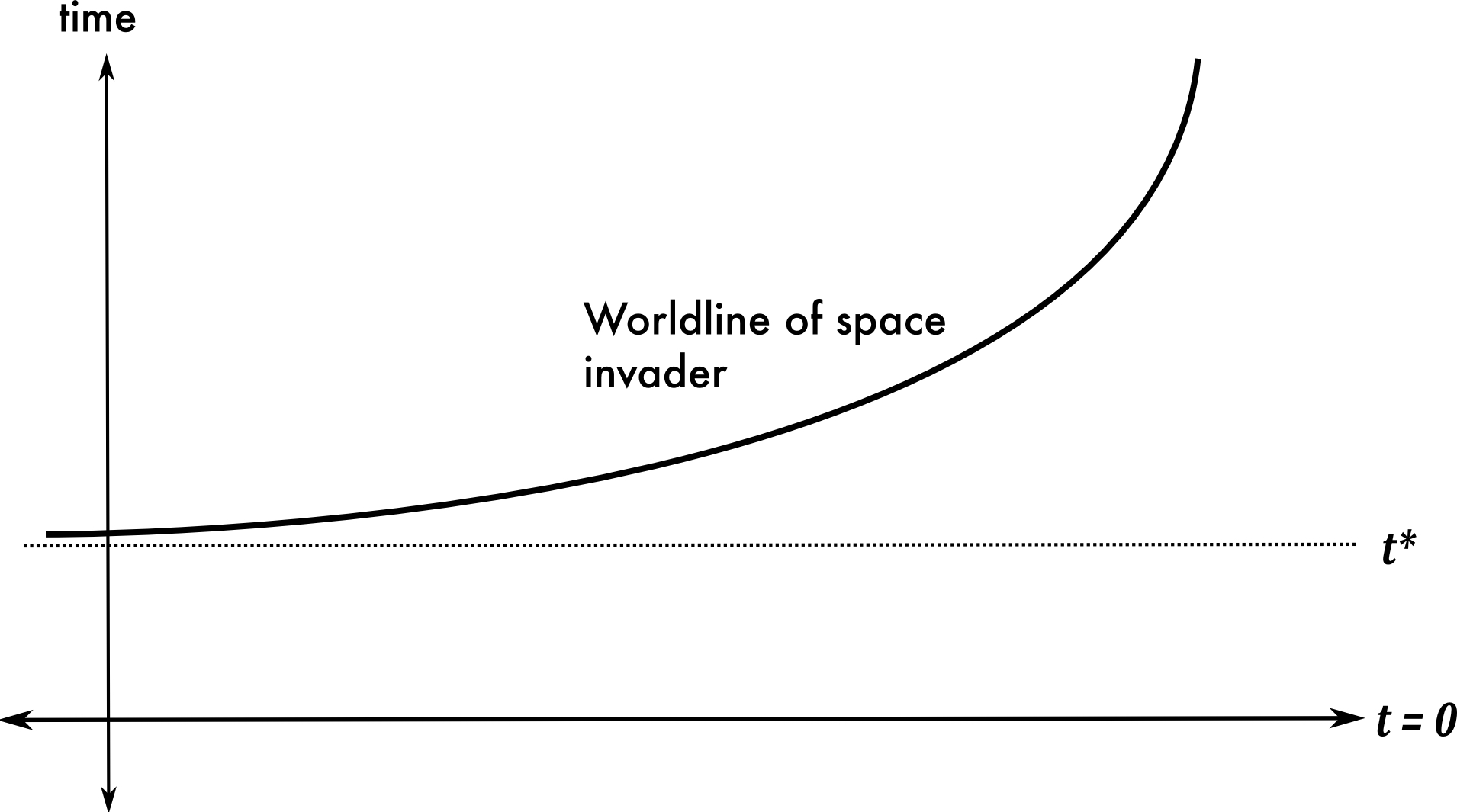
Figure 3: A ‘space invader’ comes in from spatial infinityClearly, a world with a space invader does fail to be deterministic. Before t = t*, there was nothing in the state of things to enable the prediction of the appearance of the invader at t = t* +.[2] One might think that the infinity of space is to blame for this strange behavior, but this is not obviously correct. In finite, “rolled-up” or cylindrical versions of Newtonian space-time space-invader trajectories can be constructed, though whether a “reasonable” mechanism to power them exists is not clear.[3]A second class of determinism-breaking models can be constructed on the basis of collision phenomena. The first problem is that of multiple-particle collisions for which Newtonian particle mechanics simply does not have a prescription for what happens. (Consider three identical point-particles approaching each other at 120 degree angles and colliding simultaneously. That they bounce back along their approach trajectories is possible; but it is equally possible for them to bounce in other directions (again with 120 degree angles between their paths), so long as momentum conservation is respected.)Moreover, there is a burgeoning literature of physical or quasi-physical systems, usually set in the context of classical physics, that carry out supertasks (see Earman and Norton (1998) and the entry on supertasks for a review). Frequently, the puzzle presented is to decide, on the basis of the well-defined behavior before time t = a, what state the system will be in at t = a itself. A failure of CM to dictate a well-defined result can then be seen as a failure of determinism.In supertasks, one frequently encounters infinite numbers of particles, infinite (or unbounded) mass densities, and other dubious infinitary phenomena. Coupled with some of the other breakdowns of determinism in CM, one begins to get a sense that most, if not all, breakdowns of determinism rely on some combination of the following set of (physically) dubious mathematical notions: {infinite space; unbounded velocity; continuity; point-particles; singular fields}. The trouble is, it is difficult to imagine any recognizable physics (much less CM) that eschews everything in the set.
Figure 4: A ball may spontaneously start sliding down this dome, with no violation of Newton's laws. (Reproduced courtesy of John D. Norton and Philosopher's Imprint)Finally, an elegant example of apparent violation of determinism in classical physics has been created by John Norton (2003). As illustrated in Figure 4, imagine a ball sitting at the apex of a frictionless dome whose equation is specified as a function of radial distance from the apex point. This rest-state is our initial condition for the system; what should its future behavior be? Clearly one solution is for the ball to remain at rest at the apex indefinitely.But curiously, this is not the only solution under standard Newtonian laws. The ball may also start into motion sliding down the dome—at any moment in time, and in any radial direction. This example displays “uncaused motion” without, Norton argues, any violation of Newton's laws, including the First Law. And it does not, unlike some supertask examples, require an infinity of particles. Still, many philosophers are uncomfortable with the moral Norton draws from his dome example, and point out reasons for questioning the dome's status as a Newtonian system (see e.g. Malament (2007)). | |
|
